alpinebion.blogg.se - Circles in rectangle optimization w radius of 2

All natural numbers N have their corresponding root operations, which we call the Nth root. The same semantical problem persists with the reverse terms square root and cube root. They are just abbreviations for multiplication operations and have nothing to do with geometrical shapes and exist independently from geometry and area/volume calculations. Wait a minute! Exponents b 2 and b 3 are mathematical operations from the Algebra Department. Similarly, the expression b 3 = b ⋅ b ⋅ b is called "the cube of b" or " b cubed", because the volume of a cube with side-length b is b 3. “The expression b 2 = b ⋅ b is called "the square of b" or " b squared", because the area of a square with side-length b is b 2. Here is how Wikipedia explains this exponentiation phenomenon: However, besides 2 and 3, we treat all other exponents N p equally by saying "N to the power of p". Have you ever noticed that we call a number to the power of 2 as the number squared? Similarly, we call a number to the power of 3 as the number cubed.

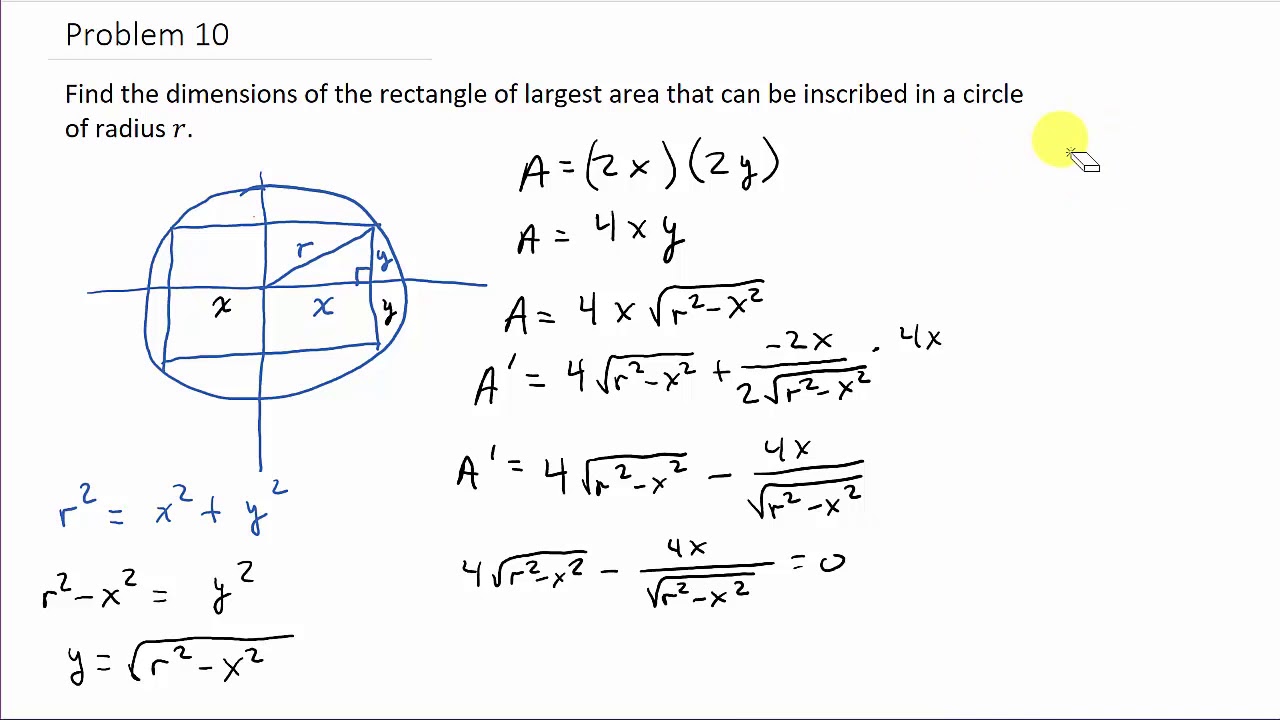
Let’s start with some questionable and overreaching semantics in algebra. (Definition: A misnomer is a wrong or inaccurate use of a name or term.) Wanna know how? Just sit down, relax, open your mind and fasten your seat belt. In this post, I dare to debunk the notion of π being an inherent component of the omnipresent circle area and sphere volumes formulas:īelieve it or not, we can significantly simplify these formulas by getting rid of π altogether. While it is impossible to overstate the significance of π in its fundamental and legendary role of being a constant representing the circumference/diameter ratio, its usage for area and volume measurements is not as much of a “settled science” as you may think. Therefore, we can derive a circle's circumference C from its diameter d using the following famous formula: This date in the format MM/DD is 3/14 which corresponds to the first three digits of the π value 3.14.Īs you all know, π represents the ratio of a circle's circumference to its diameter.

Given height and volume calculate the radius, lateral surface area and total surface area.Every year on March 14, we celebrate Pi Day in recognition of the famed mathematical constant π.

Given height and lateral surface area calculate the radius, volume and total surface area.

Given radius and lateral surface area calculate the height, volume and total surface area.

Given radius and volume calculate the height, lateral surface area and total surface area.

Given radius and height calculate the volume, lateral surface area and total surface area.

Use the following additional formulas along with the formulas above. You can do this using theĬircle calculator. To calculate the total surface area you will need to also calculate the area of the top and bottom. ** The area calculated is only the lateral surface of the outer cylinder wall.

Total surface area of a closed cylinder is:.

Calculate the top and bottom surface area of a cylinder (2.

Calculate the lateral surface area of a cylinder (just the curved outside)**:.

Calculations are based on algebraic manipulation of these standard formulas. For example, if you are starting with mm and you know r and h in mm, your calculations will result with V in mm 3, L in mm 2, T in mm 2, B in mm 2 and A in mm 2.īelow are the standard formulas for a cylinder. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. Units: Note that units are shown for convenience but do not affect the calculations. This is a right circular cylinder where the top and bottom surfaces are parallel but it is commonly referred to as a "cylinder." It will also calculate those properties in terms of PI π. This online calculator will calculate the various properties of a cylinder given 2 known values.